I'm Dan Gould

The Ben-Or, Goldwasser, and Widgerson SFE Protocol

Purpose

The Ben-Or, Goldwasser, and Widgerson protocol [1] allows for multi-party secure function evaluation in an environment relying on:

  • Honest but curious operation: Honest in that every party is obliged to follow the protocol. Curious in that all parties try to find out as much about the other parties as possible.[2]
  • Pairwise secure channels which exist between parties
  • Synchronous communication: Each party waits until it receives all messages for a given round before sending messages for the next round.

let $f$ be an $n$-input function, and consider $n$ parties $P_1, \dots, P_n$ where each party $P_i$ has input $x_i$. A protocol for secure evaluation of $f$ should satisfy the following requirements:

  • Correctness: For a given function $f$, parties collectively, on any input $x_i,\dots ,x_n$, output $f(x_1,\dots,x_n)$
  • $(n, t)$ Secrecy: The goal is for individual function inputs to stay private. No private information should be revealed by the operation of the protocol. That is, any information that any coalition $C$ of less than $t$ parties is able to infer from interacting with the protocol it would be able to infer from just the inputs and outputs of these parties alone. That is:

$$\forall (x_1, ..., x_n), (x'_1, ..., x'_n)$$ $$\forall C \in N \leftarrow \{ 1, ..., n \}$$ such that $$|C| \lt t$$ such that $$\forall i \in C$$ $$x_i = x'_i, f(x_1, ..., x_n) = f(x'_1, ..., x'_n)$$ $$\text{View}_\pi(C, (x_1, ..., x_n)) = \text{View}_\pi(C, (x'_1, ..., x'_n))$$

Any coalition of parties $C$ with fewer than $t$ members, upon changing their input or otherwise operating learns no new information. BGW is meant and able to evaluate algebraic circuits. Any boolean circuit can be transformed into an algebraic circuit by replacing $x \wedge y$ with $xy$ and $x \vee y$ with $x + y - xy$ [3]. Addition at no cost, multiplication at $O(n^2)$ cost.

Shamir Secret Sharing

Let $s$ be a secret. We review t-out-of-n secret sharing denoted $(n, t)$. That is, any $t$ of $n$ parties can reconstruct the secret but $t-1$ cannot[3][4] furthermore, the view of any coalition of $t-1$ or fewer parties should grant no more information to its view than that of a single secret share.

For a $(n, t)$ Shamir secret scheme shared among $n$ parties with $t$ secrecy, random coefficients $r$ of a degree $t-1$ polynomial are generated such that $f(0) = s$ and $s$ is the secret: $\bar{r} := (r_1, ..., r_t) \in_R G$. The $t$ coefficients can then be the constructed as the secret polynomial $A$: $$A(x) = s + r_1 x + ... + r_{t} x^{t}$$ Secret shares $\alpha_i$, which are really points on this polynomial, are then sent to each of the $n$ participants from the total set $\alpha_i := A(i)$.

In practice, modular arithmetic is used to allow shares to be sourced from a finite field $\mathbb{F}_q$ where $n \lt q$ rather than relying on a continuous line of the polynomial $A$. Any degree $t-1$ polynomial can be exactly described by $t$ points, so each party is given a point in the finite field where $t$ of them are used to construct the original and secret point. Each point is a share $s_i$ given to each user, of the complete secret. In this case, it follows that $s \in \mathbb{F}_q$ as well.

The original secret is finally reconstructed from the key fragments by calculating Lagrange polynomial of the shares in a step called interpolation. This polynomial interpolation is calculated as follows:

$$s = f(0) = \sum\limits_{i=1}^{n} \lambda_{i}\alpha_i$$ where $$\lambda_{i} = \frac{\prod_{j=1,j\not{=}i}^n (0 - \alpha_j)}{\prod_{j=1,j\not{=}i}^n (\alpha_i - \alpha_j)}$$ These $\lambda_i$ lambdas are fixed and public values. They depend only on the finite field $\mathbb{F}_q$, $t$, $n$, and $i$.

Secrecy

Theorem: knowledge of any $t-1$ or fewer secret shares leaves no more information about $s$ than having $0$ shares. $t$ or more shares allow for easy computation of $s$.[4]

Proof.

  1. The view of a coalition of $t-1$ parties consists of as many values from the polynomial $A$ of degree $t$ at $t-1$ points.
  2. Such values describe any number of degree $t-1$ polynomials. For example (figure 1): any number of quadratic functions can pass through two points. Only when 3 values are provided is an exact quadratic polynomial described.
  3. Therefore, because every possible value of $s$ within the finite field is equally likely (as each polynomial is equally likely) as much knowledge is known with $t-1$ shares as is with $0$ shares.
□
2 points describe infinite quadratic functions[5]

Shamir Interpolation as a Linear Function

When multiplying two shares of degree $t$, the degree of the resulting polynomial is of degree $2t$. This higher degree would make it so the shares cannot later be decoded, so the Legrange coefficient is multiplied by the resulting multiplication to reduce the degree of the product while retaining its essence. This is detailed in the protocol section. $$\text{Pr}[a_1, ..., a_t \leftarrow_R F_q, V^{-1} \cdot \begin{bmatrix} s\\ a_1 \\ ... \\ a_t \\ 0 \end{bmatrix} = \alpha_1, ... \alpha_t] = \frac{1}{q^t} \text{ for independent s.}$$

$V$ is an $n$-by-$n$ Vandermonde matrix ($V=[v_{i,j}]_{i,j\in1..n}, v_{i,j} = i^j$), and $\alpha_i$ is the coefficient of the $i^{\text{th}}$ degree term of $A(x)$. A Vandermonde matrix is one containing the terms of a geometric progression in each row. In this case, it contains the variable part of each term of the polynomial. Inversion of this matrix allows for interpolation and discovery of the original polynomial.

Secret Share Homomorphism

Shamir secret shares are homomorphic because they are coefficients of polynomials. This property allows computation to be done on each share locally while the underlying structure is preserved. For example, if the following functions $f$ and $g$ are homomorphic then it follows: $$f(g(x)) = g(f(x))$$

In the case of secret shares, as long as the degree of the underlying secret polynomial is maintained, the shares can be further manipulated. This is why addition can be done between shares locally with no extra cost other than that of computing direct addition: $ax + bx = (a+b)x$. In the case shares are multiplied, an extra step must be explained to keep the degree of the result from changing because $ax \cdot bx = (a \cdot b)x^2$.

The BGW Protocol

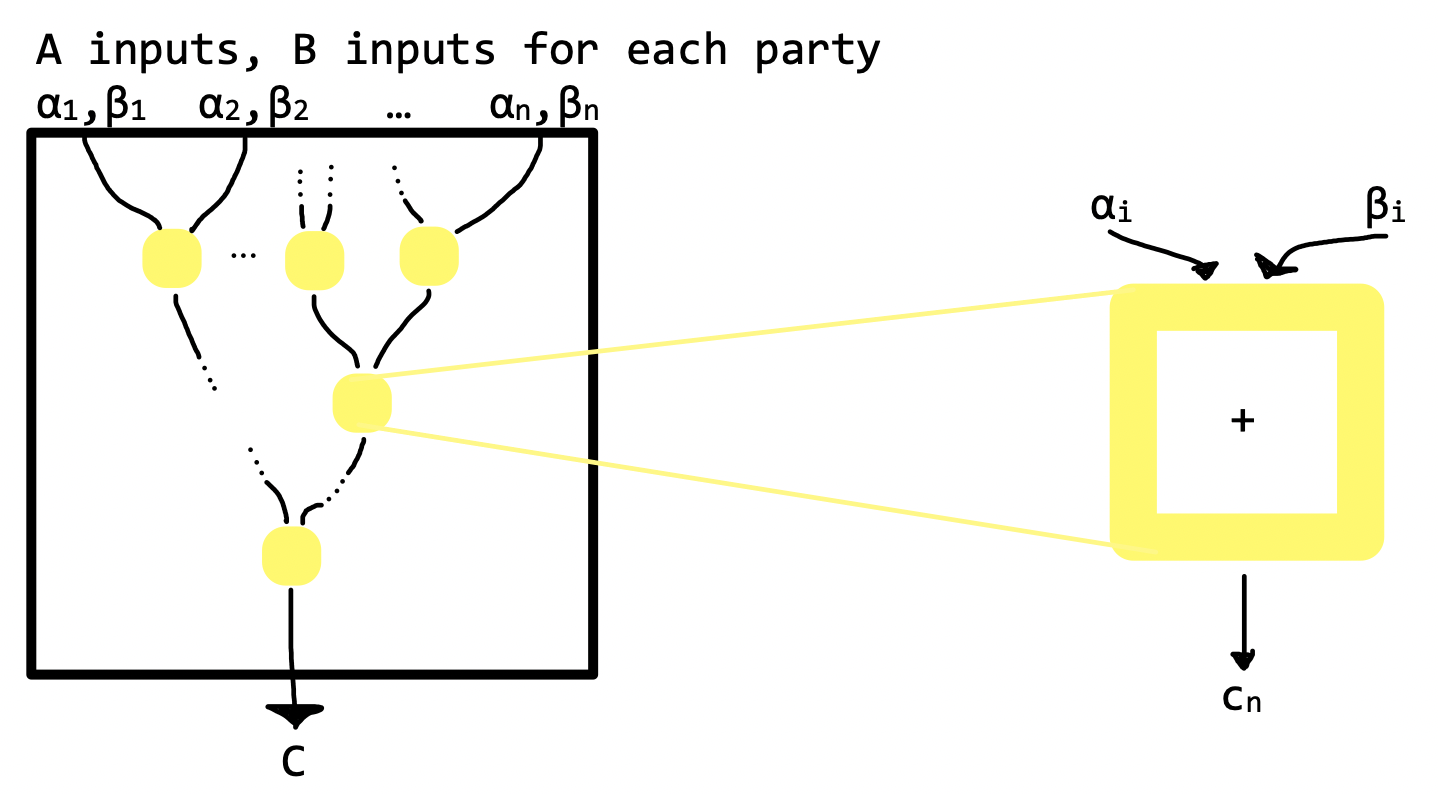
Example BGW protocol evaluating addition

$t := \lfloor \frac{n-1}{2} \rfloor$ for each party in $n$, broadcast $n$ input values $x_1, \dots, x_n$ via shamir polynomial with degree $t$ Each gate is evaluated in topological order.

Evaluating an Addition Gate $c = \alpha + \beta$

$A$, $B$ inputs are shared in an $t + 1$ out of $n$ via Shamir. $A = \{\alpha_1, \dots, \alpha_n\}, B = \{\beta_1, \dots, \beta_n\}$ Because the degree of a polynomial is equal to the greater of the addends’ degree, and each is of degree $t-1$, each share of the solution may be computed locally as $c_i = \alpha_i + \beta_i$ and then finally shared to the group for a final output $C$

Evaluating an multiplication gate $\delta = \alpha \cdot \beta$

Multiplication of polynomials changes the degree of the polynomial. To combat this, multiplication gates require a bit more trickery than addition. Each product is first evaluated locally as $\delta_i = \alpha_i \cdot \beta_i$. The resulting vector of points $D$ describes points on a polynomial $D(x) = \delta_0+\delta_1x+...+\delta_{2t}x^{2t}$ of degree $2t$ such that $D(0) = A(0) \cdot B(0)$. Linear interpolation is used, as in secret sharing, to bring $D$ to degree $t$ while retaining the essence of the product evaluation. Because $2t+1 \lt n$, $n$ parties can interpolate $D$. We define the polynomial $E_i(x) = e_0+e_1x+...+e_{t}x^{t}$. $E_i(x)$ is the polynomial used by $P_i$ to re-share its share $\delta_i$. That is, $E_i(0) = \delta_i$. The coefficients of $E_i$ are random, except for the free coefficient $\delta_i$. To split each $\delta_i$ into shares $n$ can interpolate, $t$ distinct random values within the range of $E$ $\epsilon_{i1}, \dots, \epsilon_{it}$ are selected in the same way as for secret sharing for each $\delta_i$ chosen by party $i$. $\epsilon_{ij} = E_i(j)$. Each party receives shares for each “row” e.g. $\epsilon_{1j}, \dots, \epsilon_{nj}$ and combines them into $\gamma_j$, whose values may be finally interpolated using the Lagrange coefficients as the output of the circuit. $$ \begin{align*} & \{ \delta_1, \;\;\, \delta_2, \;\dots, \;\,\, \delta_n \} \\ & \{ \epsilon_{11}, \epsilon_{21},\; \dots,\; \epsilon_{n1} \} \\ \gamma_j = \sum\limits_{i = 1}^{n} \lambda_i\epsilon_{ij} \leftarrow & \{ \bullet, \quad \bullet, \;\;\; \dots, \quad \bullet \,\} \\ &\{ \qquad\ \; \ \quad\dots \qquad \} \\ & \{ \bullet, \quad \bullet, \;\;\; \dots, \quad \bullet \,\} \\ \gamma_n = \sum\limits_{i = 1}^{n} \lambda_i\epsilon_{in} \leftarrow & \{ \epsilon_{1n}, \epsilon_{2n}, \dots, \;\epsilon_{nn} \} \end{align*} $$ $$\delta_0 = A \cdot B = \sum\limits_{i=1}^{n} \lambda_i\gamma_i = \sum\limits_{i=1}^{n} \lambda_i\sum\limits_{j=1}^{n} \lambda_j\epsilon_{ij}$$

Correctness of Multiplication via Multi-Party Gate

Know: $$ \begin{align*} \gamma &= \sum\limits_{i=1}^{n} \lambda_i\delta_i \\ \end{align*} $$ Proof. $$ \begin{align*} \gamma &= \sum\limits_{i=1}^{n} \lambda_i \gamma_i \\ &= \sum\limits_{i=1}^{n} \lambda_i [\sum\limits_{j=1}^n \lambda_j E_j(i)] \\ &= \sum\limits_{i=1}^{n} \lambda_i [E_i(0)] \\ &= \sum\limits_{i=1}^{n} \lambda_i \delta_i \\ \end{align*} $$ $$ \text{Pr}[\text{View}_\pi(C, (x_1, ... , x_n)) = v_0] = \frac{1}{F^{t \cdot m}} $$

□

Interpolate Shares

Finally, the shared polynomial of degree $t$ is interpolated as secret shares as outlined in the secret sharing section. This value refers to the final output wire of the entire circuit.

Secrecy

As described to begin with, function inputs must remain private. For any coalition of $t-1$ or fewer parties, and for any two inputs to all parties such that the outputs of the parties in the coalition are the same on both inputs, the view of the coalition from an execution on one input has the same distribution as its view from an execution on the other input. This is because the input secret shares come from an equal distribution out of a finite field as detailed in the secret sharing section. The following describes a general way to represent the protocol execution in the presence of an adversarial environment and the security in such a setting:

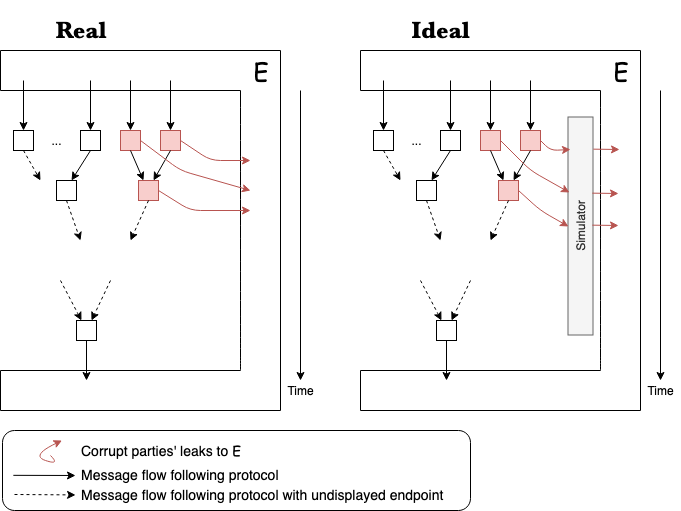
In a real scenario, it is possible some of the parties leak information at intermediate steps to the external environment $E$. This is not a problem for secrecy, because as long as the number of corrupt parties is less than $t$, no information beyond the initial information is to be gained. The corrupt parties may share one another’s input, but that is out of choice and no fault of the protocol.

In an ideal world, there exists some simulator which corrupt parties would unknowingly leak their secrets to. This simulator has the capability to sample shares and leak them to the environment in such a way that the environment is unaware of the simulator’s existence. This is possible because secret shares are created in such a way that every possible share from the finite field they are source from is equally likely. The shares are indistinguishable from random. This is the security the protocol relies on.

The same security model is used for the secret sharing protocol itself for the same reason. Though not flowing through circuits, secret shares require $t$ parties to put the secret back together.

References